PEDRO LIRIA, IRATI EPELDE, ASIER NIETO investigadores y ARITZ ABALIA estudiante de doctorado del área de Oceanografía operacional

Conocer las condiciones del oleaje y poder medir la altura de la ola en rotura es muy importante de cara a establecer el nivel de impacto del oleaje en la costa durante los temporales. Sin embargo, no siempre resulta una tarea sencilla.

Para poder dar una respuesta a esta necesidad, en el marco del proyecto Interreg POCTEFA MARLIT se ha desarrollado un algoritmo que permite medir el oleaje a partir de las imágenes obtenidas por los sistemas de videometría KOSTASystem. Así, a través de los sistemas de observación podemos mejorar y automatizar las herramientas de gestión de riesgos costeros y permitir la caracterización de los impactos asociados a los temporales.

Las ventajas de los sistemas de videometría

Un sistema de videometría costera consiste en cámaras instaladas en la costa que permiten la captación de imágenes y su referenciación espacial. Hasta ahora se utilizaban para el seguimiento de la configuración morfológica de las playas, dunas, canales y barras, pero en los últimos años se han realizado importantes avances en la capacidad de estos sistemas para obtener información fiable de las condiciones del mar y concretamente de la caracterización del oleaje en las playas.

Los sistemas de videometría costera procesan las imágenes que se capturan en alta frecuencia a intervalos regulares. Los productos más comunes derivados del procesado de dichas imágenes son la media, la varianza de los valores de intensidad en cada pixel o la acumulación de la información de determinadas zonas de la imagen. De cara a la caracterización del oleaje, las aproximaciones existentes, se centran en el análisis de productos generados por acumulación denominados timestack. Dichas imágenes son el resultado de la composición obtenida a partir de la acumulación sucesiva de los pixeles situados a lo largo de una línea predefinida, durante un intervalo de tiempo y con una frecuencia determinada. En la Figura 1 se muestra una imagen tomada por una de las cámaras del sistema instalado en Mundaka, y el resultado del procesado de una imagen timestack a partir del perfil resaltado mediante una línea roja en dicha imagen. Así, en estas imágenes, las filas de píxeles representan la evolución de un píxel de la imagen a lo largo del tiempo, mientras que las columnas, representan un transecto de píxeles en un instante dado.

medicion de oleaje
Figura 1. Ejemplo de imagen obtenida por el sistema Kostasystem en Mundaka.

En este sentido, en el marco del proyecto MARLIT se ha realizado un desarrollo informático que permite obtener diferentes parámetros estadísticos y espectrales del oleaje a partir del procesado de las imágenes timestack, entre los que están, el periodo del oleaje y la altura de ola en rotura y sin romper.

Metodología

Existen diferentes antecedentes de análisis de imágenes timestack para obtener parámetros del oleaje. Como más relevantes se puede citar los de Gal et al., 2011; Shand et al., 2012; Almar et al. 2012 y Colvin et al., 2020.

Estimación del periodo del oleaje

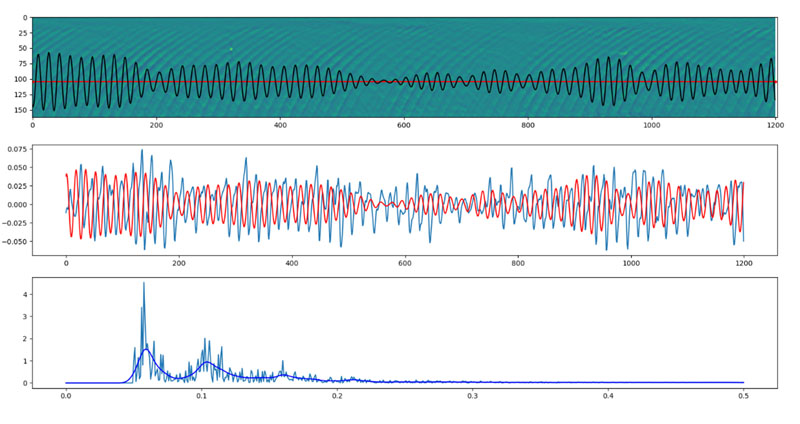
Para analizar el periodo representativo del oleaje (periodo de pico, Tp), se aplica la transformada de Fourier a la señal de intensidad obtenida en una fila de píxeles de la imagen timestack. Un ejemplo de dicho análisis se muestra en la Figura 2. En la figura superior en rojo se muestra la línea de píxeles en la cual se lleva a cabo el análisis y en negro, la señal obtenida. En la figura central se muestra en azul la señal de intensidad obtenida, y en rojo la señal procesada. En la figura inferior se muestra la distribución de frecuencias, obtenida por el análisis de Fourier. Para este análisis se define previamente una zona de la timestack que se estima como previa a la rotura y este proceso se realiza en varias líneas de pixeles y como resultado se selecciona la más recurrente (periodo de pico). Mediante la relación frecuencia-periodo (T=1/f) se obtiene el periodo dominante del oleaje.

Figura 2. Estimación de la frecuencia del oleaje en una imagen timestack de la playa de Mundaka. Arriba en rojo, la línea de píxeles en la cual se lleva a cabo el análisis, en negro, la señal obtenida. En medio en azul, la señal de frecuencias obtenida, y en rojo la señal filtrada. Abajo, frecuencias agrupadas.

Estimación de la altura de ola

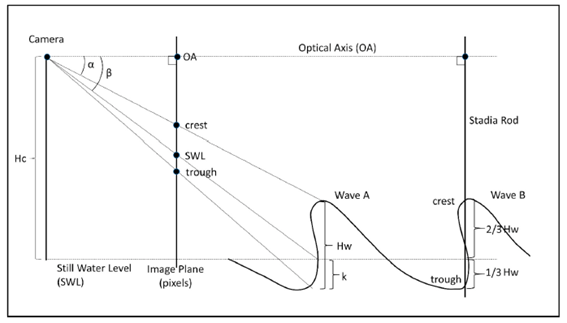
La obtención de las alturas de ola necesita de la comprensión de la geometría del caso de estudio. En la Figura 3 se muestra el esquema del oleaje y la cámara, Colvin et al., 2020. En base a dicho esquema, en el que se supone una posición de la cámara frontal a la dirección de avance del oleaje, determinando la localización de los píxeles de la cresta y el seno del oleaje es posible delimitar la altura de ola. Además, en base a la georreferenciación de la imagen, es posible obtener la altura de ola en metros a partir de los valores en píxeles de la imagen.

Figura 3. Geometría de la cámara y el oleaje. Colvin et al., 2020.

Aplicando dicho esquema en una imagen timestack, tal y como se muestra en Colvin et al., 2020, la cresta y el seno de cada ola quedan representadas en la Figura 4, siendo la cresta el punto más alto de la cara oscura de la ola, y el seno, el punto más bajo, en un instante (columna).

Figura 4. Cresta y seno del oleaje en una imagen timestack. Colvin et al., 2020.

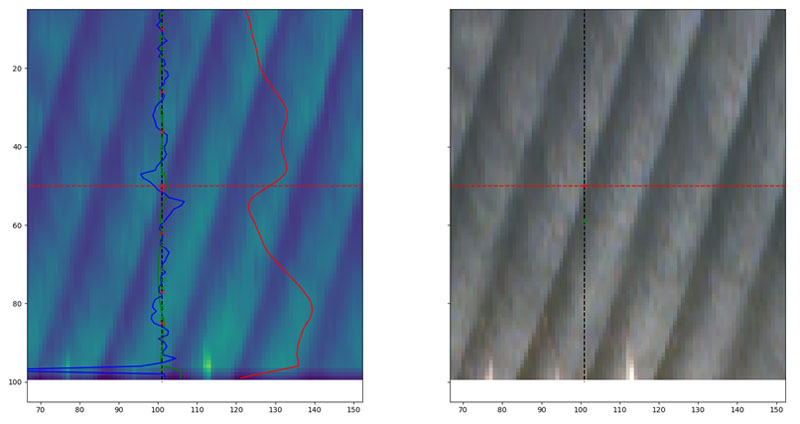
En nuestro caso de estudio, para llevar a cabo la detección automática tanto de la cresta como del seno de la ola, en el desarrollo del algoritmo se analiza para cada columna de píxeles (instante t) la variación en los 3 canales (RGB) de la imagen timestack de la playa de Mundaka. Este análisis se muestra en la Figura 5 (izquierda). En la imagen de la derecha, el punto rojo representa la cresta de la ola, mientras que el punto verde presenta el seno, ambos detectados automáticamente.

Figura 5. Estimación de la altura de ola en una timestack de la playa de Mundaka. Izquierda, zoom de la imagen timestack, donde, la línea roja, verde y azul representan la variación de cada uno de los canales de la imagen. Derecha, detección de la cresta y el seno de la ola en base a la imagen de la izquierda, punto rojo, cresta, punto verde, seno.

Estimación de la altura de ola en rotura

Al igual que la altura de ola, la altura de ola en rotura se obtiene calculando la diferencia entre la cresta y el seno de la ola, aunque, en este caso, su detección es distinta. Para una correcta comprensión, se muestra el ejemplo de Gal et al., 2011 en la timestack de la Figura 6. Así, la cresta y el seno de cada ola en el instante en el que empieza a romper queda representado en dicha figura, donde la cresta es el punto más alto de la zona blanca (rotura), y el seno, el punto más bajo, en un instante (columna).

Figura 6. Cresta y seno del oleaje en rotura en una imagen timestack. Gal et al., 2011.

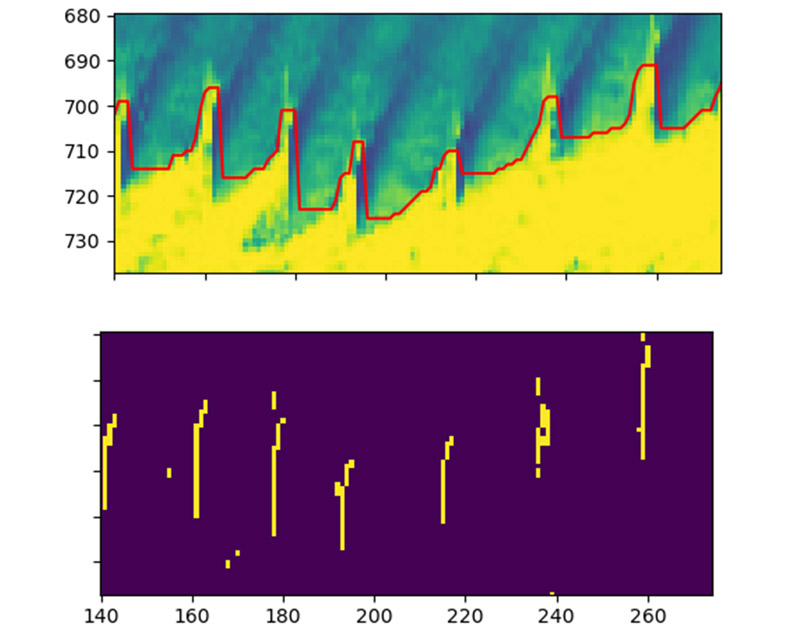
En la Figura 7 se muestra la estrategia empleada en el desarrollo del algoritmo para la detección automática de la cresta y el seno de la ola en el instante de la rotura, en el caso de estudio, en una imagen timestack de la playa de Mundaka. En la Figura 7 (arriba), se muestra la envolvente de la zona de rotura, obtenida como límite de la zona de mayor intensidad de la imagen. En la imagen 7 (abajo), se muestra la detección de la cara de la rotura, de donde se obtiene la cresta (punto más alto) y el seno (punto más bajo).

Figura 7. Estimación de la altura de ola en rotura en una timestack de la playa de Mundaka mediante el algoritmo desarrollado. Arriba, zoom de la imagen timestack, donde, la línea roja, representa la envolvente de la zona de rotura. Abajo, detección de la cara de la ola en rotura.

Ejemplos

Partiendo de una imagen timestack (Figura 8) de la playa de Mundaka, en la cual se aplica el algoritmo desarrollado, se obtienen los parámetros de periodo, altura de ola y altura de ola en rotura. Estos parámetros quedan representados en la Figura 9. De las alturas de ola obtenidas en la imagen, se obtiene el valor de altura de ola significante (H1/3), calculando la media de las alturas de ola del tercio con valores más altos. Por otro lado, de las alturas de ola en rotura medidas en la imagen y en base a la relación entre el número total de olas en la imagen con el número de olas rotas, se obtiene, la altura de ola significante (H1/3) equivalente, en el punto de rotura.

Figura 8. Ejemplo de imagen timestack obtenida por el sistema KOSTASystem en la playa de Mundaka, 17 de noviembre de 2021 a las 9:00.
Figura 9. Imagen timestack procesada con el algoritmo en la playa de Mundaka, 17 de noviembre de 2021 a las 9:00. La línea azul representa la fila de píxeles donde se ha analizado la frecuencia del oleaje, la línea naranja representa la señal de la frecuencia, los puntos negros muestran la posición de la cresta de las olas rotas y sin romper, mientras que los puntos rojos muestran la posición del seno de las olas rotas y sin romper.

Aplicando este procedimiento a una serie de imágenes, pertenecientes a varios días, se obtienen los valores mostrados en la Tabla 1. En esta misma tabla, se muestran los parámetros medidos por la boya de oleaje de Bilbao-Vizcaya (Puertos del Estado, http://www.puertos.es, 3.08W, 43.63N, 1990-2021) en el mismo instante.

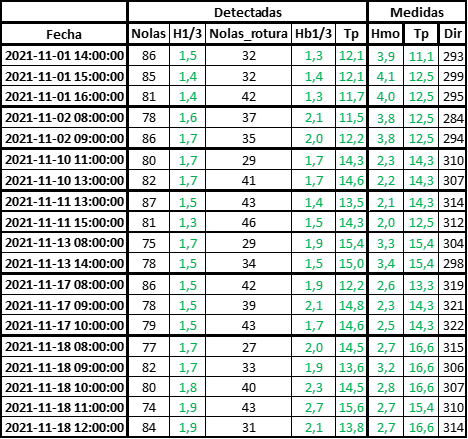
Tabla 1. Número de olas en la imagen (Nolas), valores de altura de ola significante (H1/3), número de olas rotas (Nolas_rotura), altura de ola significante en rotura (Hb1/3), periodo de pico del oleaje (Tp), altura de ola significante en aguas profundas (Hmo) y periodo de pico del oleaje en aguas profundas (Tp).

En la tabla se aprecia que, de manera general, el periodo del oleaje, el número de olas, la altura de ola y la altura de ola en rotura obtenidas en las imágenes muestran una buena concordancia entre sí, así como, una buena correspondencia con los datos de oleaje medidos en aguas profundas. En este sentido se observa muy bien como debido a la orientación norte de Mundaka protegida del noroeste por el cabo Matxitxako, aunque el periodo dominante se mantiene, los oleajes con mayor componente oeste dan alturas de ola comparativamente menores respecto a la altura en aguas profundas, que los oleajes de mayor periodo y una mayor componente norte. Esto coincide plenamente con lo esperado y parece corroborar la bondad de los datos obtenidos a partir del análisis de las imágenes, aunque para una verificación mas fiable seria necesario realizar medidas directas en el entorno del punto de análisis.  

Conclusiones

La detección de parámetros del oleaje mediante imágenes timestack tiene como principales antecedentes los trabajos de Gal et al., 2011; Shand et al., 2012; Almar et al. 2012 y Colvin et al., 2020. En dichos trabajos se han desarrollado diferentes aproximaciones para el desarrollo de algoritmos de detección automática, en base al análisis de imágenes acumuladas de tipo timestack.

En el marco del proyecto INTERREG POCTEFA MARLIT se ha desarrollado un algoritmo que permite detectar automáticamente la altura de ola (en rotura y sin romper) y periodo del oleaje. Esta detección automática se basa principalmente en el análisis de los canales RGB de las imágenes acumuladas de tipo timestack obtenidas por los sistemas de videometría KOSTASystem (Liria et al., 2021).

El periodo representativo del oleaje se obtiene aplicando la transformada de Fourier a la señal de intensidad obtenida en una fila de píxeles de la imagen. Se aplica este proceso en varias filas sobre una banda predefinida en la imagen y se da como valor representativo el predominante (más recurrente).

La altura de ola se obtiene detectando en cada columna de píxeles (instante t) la cresta y seno de cada ola, en base a la diferencia de colores de la cara de la ola (oscuro), con la cresta y el seno de esta (color claro).

El caso de la altura de ola en rotura, se detecta la cresta y el seno de cada ola en base a la diferencia de colores entre la cara de la ola cuando empieza a romper con la zona blanca correspondiente a la ola rota.

Finalmente, la distancia calculada de altura de ola y altura de ola en rotura, se transforman de píxeles a metros en base a la georreferenciación del sistema de videometría.

En las pruebas realizadas, los resultados obtenidos de altura de ola y periodos muestran resultados plenamente coherentes con los oleajes registrados en aguas profundas, aunque sería conveniente una validación más exhaustiva con datos medidos en el entorno del punto de análisis.

A falta de una validación detallada, estos resultados resultan muy prometedores ya que permiten estimar las condiciones de oleaje de forma remota y en particular las condiciones de altura de ola en rotura, parámetro muy relevante de cara a establecer el nivel de impacto del oleaje sobre la costa durante los temporales. 

Referencias

  • Almar, R., Cienfuegos, R., Catalán, P. A., Michallet, H., Castelle, B., Bonneton, P., & Marieu, V. (2012). A new breaking wave height direct estimator from video imagery. Coastal Engineering, 61, 42-48.
  • Colvin, J., Lazarus, S., & Splitt, M. (2020). Extracting nearshore wave properties from video: A new method for coastal estuaries. Estuarine, Coastal and Shelf Science, 246, 107053.
  • Gal, Y., Browne, M., & Lane, C. (2011, December). Automatic estimation of nearshore wave height from video timestacks. In 2011 International Conference on Digital Image Computing: Techniques and Applications (pp. 364-369). IEEE.
  • Liria, P., Epelde, I., Santiago, I., Garnier, R., Abalia, A., and Mader, J. (2021). KOSTASystem, a coastal videometry technology: Development and applications. In 9th EuroGOOS
    International conference.
  • Shand, T. D., Bailey, D. G., & Shand, R. D. (2012). Automated detection of breaking wave height using an optical technique. Journal of Coastal Research, 28(3), 671-682.

MARLIT: “Medios de evaluación y Atenuación de los Riesgos costeros Locales debidos a Impactos de los Temporales”

AZTI lidera el proyecto MARLIT, una iniciativa transfronteriza que busca mejorar los mecanismos de predicción de riesgo de temporales en la costa vasca franco-española, y en la costa catalana, atendiendo a su evolución por el cambio climático. El proyecto tiene como objetivo principal mejorar el conocimiento y las herramientas disponibles para comprender los impactos de las tormentas actuales y futuras en la costa y, además, dar apoyo a las administraciones públicas en la gestión de riesgos costeros.

Además del centro tecnológico vasco, también participan la Universitat Politécnica de Catalunya, La Universidad de Pau, y el centro Rivages Protect como socios. Además, se cuenta con la colaboración de la Dirección de Atención de Emergencias y Meteorología (DAEM) del Gobierno Vasco, el Institut Cartogràfic i Geològic de Catalunya y la Comunidad de aglomeración del País Vasco.

Últimas noticias

Noticias relacionadas